某校对高三年级800名男生的身高(单位:cm)进行了统计,随机抽取的一个容量为50的样本的频率分布直方图的部分图形如图所示,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(1)估计这所学校高三年级全体男生身高180 cm以上(含180 cm)的人数;
(2)求第六组、第七组的频率并补充完整频率分布直方图;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x、y,求满足|x-y|≤5的事件概率.
相关知识点
推荐套卷
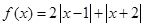 (1)求不等式
(1)求不等式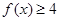 的解集;
的解集; 的解集是非空集合,求实数m的取值范围.
的解集是非空集合,求实数m的取值范围. 直线
直线
 的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;
的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;
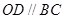 ;
;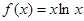 ,
,
 在
在 上的最小值;
上的最小值;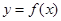 与
与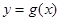 的图像恰有一个公共点,求实数a的值;
的图像恰有一个公共点,求实数a的值;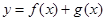 有两个不同的极值点
有两个不同的极值点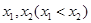 ,且
,且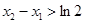 ,求实数a的取值范围。
,求实数a的取值范围。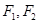 是椭圆的左、右焦点,O为坐标原点,点P
是椭圆的左、右焦点,O为坐标原点,点P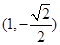 在椭圆上,线段
在椭圆上,线段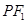 与y轴的交点M满足
与y轴的交点M满足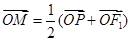
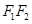 为直径的圆,直线
为直径的圆,直线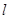 :
: 与圆相切,并与椭圆交于不同的两点
与圆相切,并与椭圆交于不同的两点 ,当
,当 ,且满足
,且满足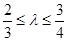 时,求直线
时,求直线 粤公网安备 44130202000953号
粤公网安备 44130202000953号