(本小题满分12分)已知斜率为1的直线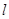 与双曲线
与双曲线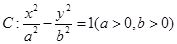 相交于B、D两点,且BD的中点为M(1,3)。
相交于B、D两点,且BD的中点为M(1,3)。
(1)求双曲线C的离心率;
(2)若双曲线C的右焦点坐标为(3,0),则以双曲线的焦点为焦点,过直线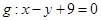 上一点M作椭圆,要使所作椭圆的长轴最短,点M应在何处?并求出此时的椭圆方程。
上一点M作椭圆,要使所作椭圆的长轴最短,点M应在何处?并求出此时的椭圆方程。
相关知识点
推荐套卷
(本小题满分12分)已知斜率为1的直线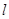 与双曲线
与双曲线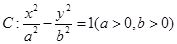 相交于B、D两点,且BD的中点为M(1,3)。
相交于B、D两点,且BD的中点为M(1,3)。
(1)求双曲线C的离心率;
(2)若双曲线C的右焦点坐标为(3,0),则以双曲线的焦点为焦点,过直线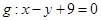 上一点M作椭圆,要使所作椭圆的长轴最短,点M应在何处?并求出此时的椭圆方程。
上一点M作椭圆,要使所作椭圆的长轴最短,点M应在何处?并求出此时的椭圆方程。