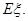(本小题满分12分)某旅行社组织了一个有36名游客的旅游团到安徽风景名胜地旅游,其中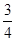 是省外游客,其余是省内游客,在省外游客中有
是省外游客,其余是省内游客,在省外游客中有 玩过黄山,在省内游客中有
玩过黄山,在省内游客中有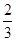 玩过黄山。
玩过黄山。
(1)在该团中随机采访3名游客,求恰有1名 省外游客玩过黄山且省内游客玩过黄山少于2人的概率;
(2)在该团的省内游客中随机采访3名游客,设其中省内游客玩过黄山的人数为随机变量 ,求
,求 的分布列及数学期望
的分布列及数学期望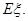
相关知识点
推荐套卷
(本小题满分12分)某旅行社组织了一个有36名游客的旅游团到安徽风景名胜地旅游,其中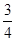 是省外游客,其余是省内游客,在省外游客中有
是省外游客,其余是省内游客,在省外游客中有 玩过黄山,在省内游客中有
玩过黄山,在省内游客中有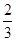 玩过黄山。
玩过黄山。
(1)在该团中随机采访3名游客,求恰有1名 省外游客玩过黄山且省内游客玩过黄山少于2人的概率;
(2)在该团的省内游客中随机采访3名游客,设其中省内游客玩过黄山的人数为随机变量 ,求
,求 的分布列及数学期望
的分布列及数学期望