（满分6分）如图的数阵是由一些奇数组成的。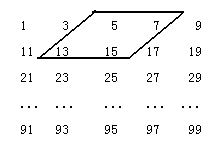
（1）形如图框中的四个数有什么关系？（可设第一行的第一个数为x，用含x的代数式表示另外三个数即可）。
（2）若这样框中的四个数的和是200，求出这四个数。
（3）是否存在这样的四个数，它们的和为2010..若存在，请求出这四个数中最大的数，若不存在请说明理由。
相关试题
益趣玩具店购进一种儿童玩具，计划每个售价36元，能盈利80﹪，在销售中出现了滞销，于
是先后两次降价，售价降为25元。
（1）求这种玩具的进价。
（2）求平均每次降价的百分率（精确到0.1﹪）。
如图1，已知菱形ABCD的边长为
，点A在x轴负半轴上，点B在坐标原点．点D的坐标为（- 
，3），抛物线y=ax2+b（a≠0）经过AB、CD两边的中点．
（1）求这条抛物线的函数解析式；
（2）将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移（如图2），过点B作BE⊥CD于点E，交抛物线于点F，连接DF、AF．设菱形ABCD平移的时间为t秒（0＜t＜ 3 ）
①是否存在这样的t，使△ADF与△DEF相似？若存在，求出t的值；若不存在，请说明理由；
②连接FC，以点F为旋转中心，将△FEC按顺时针方向旋转180°，得△FE′C′，当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中（包括边界）时，求t的取值范围．（写出答案即可）
粤公网安备 44130202000953号