出租车司机从饭店到火车站途中有六个交通岗,假设他在各交通岗到红灯这一事件是相互独立的,并且概率都是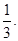
(1)求这位司机遇到红灯前,已经通过了两个交通岗的概率;
(2)求这位司机在途中遇到红灯数ξ的期望和方差。
相关知识点
推荐套卷
出租车司机从饭店到火车站途中有六个交通岗,假设他在各交通岗到红灯这一事件是相互独立的,并且概率都是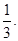
(1)求这位司机遇到红灯前,已经通过了两个交通岗的概率;
(2)求这位司机在途中遇到红灯数ξ的期望和方差。