如图,在半径为r的半圆⊙O中,半径OA⊥直径BC,点E、F分别在弦AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.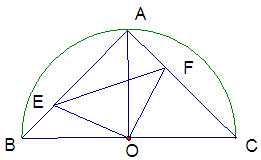
(1)求证 S四边形AEOF=
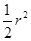 ;
;(2)设AE=x,S△OEF=y,写出y与x之间的函数关系式及自变量x的范围;
(3)当S△OEF =
 S△ABC时,求点E、F分别在AB、AC上的位置及EF的长。
S△ABC时,求点E、F分别在AB、AC上的位置及EF的长。
相关知识点
推荐套卷
如图,在半径为r的半圆⊙O中,半径OA⊥直径BC,点E、F分别在弦AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.
(1)求证 S四边形AEOF=
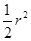 ;
;(2)设AE=x,S△OEF=y,写出y与x之间的函数关系式及自变量x的范围;
(3)当S△OEF =
 S△ABC时,求点E、F分别在AB、AC上的位置及EF的长。
S△ABC时,求点E、F分别在AB、AC上的位置及EF的长。