(本题满分10分)用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为xm,窗户的透光面积为ym2,y与x的函数图象如图2所示.(图中顶点横坐标为1,纵坐标为1.5)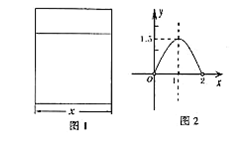
⑴写出y与x之间的函数关系式,指出当x为何值时,窗户透光面积最大?
⑵当窗户透光面积1.125m2时,窗框的两边长各是多少?
相关知识点
推荐套卷
(本题满分10分)用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为xm,窗户的透光面积为ym2,y与x的函数图象如图2所示.(图中顶点横坐标为1,纵坐标为1.5)
⑴写出y与x之间的函数关系式,指出当x为何值时,窗户透光面积最大?
⑵当窗户透光面积1.125m2时,窗框的两边长各是多少?