(本小题满分12分) 两城相距
两城相距 ,在
,在 两地之间距
两地之间距 城
城 的
的 地建一核电站给
地建一核电站给 两城供电,为保证城市安全,核电站距市距离不得少于
两城供电,为保证城市安全,核电站距市距离不得少于 .已知供电费用与供电距离的平方和供电量之积成正比,比例系数
.已知供电费用与供电距离的平方和供电量之积成正比,比例系数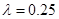 .若
.若 城供电量为
城供电量为 亿度/月,
亿度/月, 城为
城为 亿度/月.
亿度/月.
(I)把月供电总费用 表示成
表示成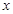 的函数,并求定义域;
的函数,并求定义域;
(II)核电站建在距 城多远,才能使供电费用最小.
城多远,才能使供电费用最小.
推荐套卷
(本小题满分12分) 两城相距
两城相距 ,在
,在 两地之间距
两地之间距 城
城 的
的 地建一核电站给
地建一核电站给 两城供电,为保证城市安全,核电站距市距离不得少于
两城供电,为保证城市安全,核电站距市距离不得少于 .已知供电费用与供电距离的平方和供电量之积成正比,比例系数
.已知供电费用与供电距离的平方和供电量之积成正比,比例系数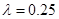 .若
.若 城供电量为
城供电量为 亿度/月,
亿度/月, 城为
城为 亿度/月.
亿度/月.
(I)把月供电总费用 表示成
表示成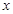 的函数,并求定义域;
的函数,并求定义域;
(II)核电站建在距 城多远,才能使供电费用最小.
城多远,才能使供电费用最小.