（（本题14分）如图3，四棱锥P—ABCD中，底面ABCD是矩形，PA⊥平面ABCD，M、N分别是AB、PC的中点，PA=AD=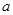
。
(Ⅰ)求证：MN//平面PAD；
(Ⅱ)求证：平面PMC⊥平面PCD；
(Ⅲ)若二面角P—MC—A是60°的二面角，求四棱锥P—ABCD的体积。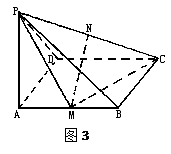
相关试题
，且
，
;
；
的值。
，求：
，求
，
的右焦点F为
，G上的点到点F的最大距离为
，斜率为1的直线
与椭圆G交与
、
两点，以AB为底边作等腰三角形，顶点为P（-3,2）
的面积。推荐套卷
（（本题14分）如图3，四棱锥P—ABCD中，底面ABCD是矩形，PA⊥平面ABCD，M、N分别是AB、PC的中点，PA=AD=。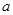
(Ⅰ)求证：MN//平面PAD；
(Ⅱ)求证：平面PMC⊥平面PCD；
(Ⅲ)若二面角P—MC—A是60°的二面角，求四棱锥P—ABCD的体积。
粤公网安备 44130202000953号