(本小题满分13分)
从甲、乙两个班中各随机的抽取6名学生,他们的数学成绩如下:
| 甲班 |
76 |
74 |
82 |
96 |
66 |
76 |
| 乙班 |
86 |
84 |
62 |
76 |
78 |
92 |
(I)画出茎叶图并求出甲班学生的数学成绩的中位数;
(II)若不低于80分则表示该生数学成绩为优秀。现从甲、乙两班中各抽出1名学生参加数学兴趣小组,求这两名学生的数学成绩恰好都优秀的概率。
推荐套卷
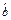 x+
x+ 的回归系数
的回归系数 粤公网安备 44130202000953号
粤公网安备 44130202000953号