本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知 的三个顶点在抛物线
的三个顶点在抛物线 :
: 上运动,
上运动,
(1). 求 的焦点坐标;
的焦点坐标;
(2). 若点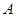 在坐标原点, 且
在坐标原点, 且 ,点
,点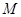 在
在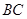 上,且
上,且  ,
,
求点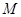 的轨迹方程;
的轨迹方程;
(3). 试研究: 是否存在一条边所在直线的斜率为 的正三角形
的正三角形 ,若存在,求出这个正三角形
,若存在,求出这个正三角形 的边长,若不存在,说明理由.
的边长,若不存在,说明理由.
相关知识点
推荐套卷
本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知 的三个顶点在抛物线
的三个顶点在抛物线 :
: 上运动,
上运动,
(1). 求 的焦点坐标;
的焦点坐标;
(2). 若点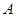 在坐标原点, 且
在坐标原点, 且 ,点
,点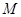 在
在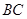 上,且
上,且  ,
,
求点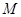 的轨迹方程;
的轨迹方程;
(3). 试研究: 是否存在一条边所在直线的斜率为 的正三角形
的正三角形 ,若存在,求出这个正三角形
,若存在,求出这个正三角形 的边长,若不存在,说明理由.
的边长,若不存在,说明理由.