(本题满分18分,其中第1小题4分,第2小题6分,第,3小题8分)
一青蛙从点 开始依次水平向右和竖直向上跳动,其落点坐标依次是
开始依次水平向右和竖直向上跳动,其落点坐标依次是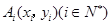 ,(如图所示,
,(如图所示,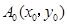 坐标以已知条件为准),
坐标以已知条件为准),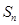 表示青蛙从点
表示青蛙从点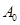 到点
到点 所经过的路程。
所经过的路程。
(1) 若点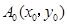 为抛物线
为抛物线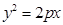
 准线上
准线上
一点,点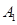 ,
,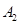 均在该抛物线上,并且直线
均在该抛物线上,并且直线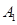
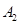 经
经
过该抛物线的焦点,证明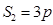 .
.
(2)若点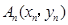 要么落在
要么落在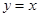 所表示的曲线上,
所表示的曲线上,
要么落在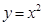 所表示的曲线上,并且
所表示的曲线上,并且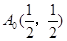 ,
,
试写出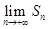 (不需证明);
(不需证明);
(3)若点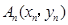 要么落在
要么落在 所表示的曲线上,要么落在
所表示的曲线上,要么落在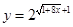 所表示的曲线上,并且
所表示的曲线上,并且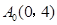 ,求
,求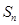 的表达式.
的表达式.
推荐套卷
 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第 个1和第
个1和第 个1之间有
个1之间有 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前 项的和为
项的和为 .
. 和
和 ;
; ,使得
,使得 ?如果存在,求出
?如果存在,求出 .
. 的分布列及数学期望
的分布列及数学期望 ;
; 元,而且每赛一场追加服务费
元,而且每赛一场追加服务费 元,那么举行一次这样的比赛,预计平均花费多少元?
元,那么举行一次这样的比赛,预计平均花费多少元? 为实数,证明:
为实数,证明: .
. ,
,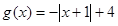 .
. 的值不大于
的值不大于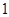 ,求
,求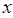 的取值范围;
的取值范围; 的解集为
的解集为 ,求
,求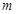 的取值范围.
的取值范围. 内,直线
内,直线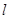 的参数方程
的参数方程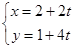 (
(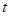 为参数),以
为参数),以 为极轴建立极坐标系,圆
为极轴建立极坐标系,圆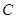 的极坐标方程为
的极坐标方程为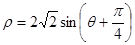 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号