本题共有2个小题，第1小题满分8分，第2小题满分6分.
为保护环境，某单位采用新工艺，把二氧化碳转化为一种可利用的化工产品。已知该单位每月的处理量最多不超过300吨，月处理成本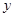
（元）与月处理量
（吨）之间的函数关系式可近似的表示为：
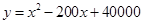，且每处理一吨二氧化碳得到可利用的化工产品价值为300元。
（1）该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？
（2）要保证该单位每月不亏损，则每月处理量应控制在什么范围？
相关试题
，直线
是圆的一条切线，且
与椭圆
交于不同的两点
．
与
的关系；
的长为
，求直线
及圆
．
过点
且被圆
截得的线段
长为
，求直线
,两个命题，
函数
在
内单调递减；
曲线
与
轴交于不同两点，如果
是假命题，
是真命题，求实数a的取值范围．
满足不等式组
，
的最大值；
的最小值．
的坐标为（1，1），圆
轴和
轴都相切．推荐套卷
本题共有2个小题，第1小题满分8分，第2小题满分6分.
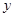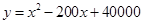为保护环境，某单位采用新工艺，把二氧化碳转化为一种可利用的化工产品。已知该单位每月的处理量最多不超过300吨，月处理成本（元）与月处理量（吨）之间的函数关系式可近似的表示为：，且每处理一吨二氧化碳得到可利用的化工产品价值为300元。
（1）该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？
（2）要保证该单位每月不亏损，则每月处理量应控制在什么范围？
粤公网安备 44130202000953号