本题共有2个小题,第1小题满分6分,第2小题满分6分.
已知复数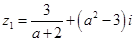 ,
,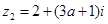 (
( ,
,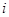 是虚数单位)。
是虚数单位)。
(1)若复数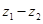 在复平面上对应点落在第一象限,求实数
在复平面上对应点落在第一象限,求实数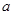 的取值范围
的取值范围
(2)若虚数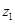 是实系数一元二次方程
是实系数一元二次方程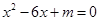 的根,求实数
的根,求实数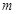 的值.
的值.
相关知识点
推荐套卷
本题共有2个小题,第1小题满分6分,第2小题满分6分.
已知复数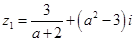 ,
,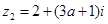 (
( ,
,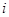 是虚数单位)。
是虚数单位)。
(1)若复数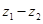 在复平面上对应点落在第一象限,求实数
在复平面上对应点落在第一象限,求实数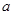 的取值范围
的取值范围
(2)若虚数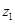 是实系数一元二次方程
是实系数一元二次方程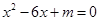 的根,求实数
的根,求实数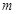 的值.
的值.