（本小题12分）如图，有五个边长为1的小正方形组成的图形纸，我们可以把它剪开后拼成一个大正方形。
拼成的大正方形的面积与边长分别是多少？
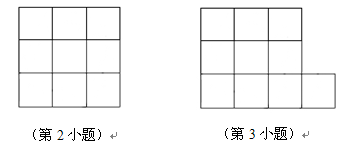
你能在下图3×3方格中，连接四个格点，组成面积为5的正方形吗？
你还能把十个小正方形组成的图形纸，剪开并拼成更大的正方形吗?若能，请在下图中画出图形，并求出它的边长是多少？
相关试题
如图，点A、B在数轴上分别表示有理数
、
，在数轴上A、B两点之间的距离
．回答下列问题：
（1）数轴上表示1和
的两点之间的距离是；
（2）数轴上表示
和的两点之间的距离表示为；
（3）若表示一个有理数，请你结合数轴求
的最小值．
=1-
， 
=
， 
=
，
=
则：
的值．
粤公网安备 44130202000953号