（本小题满分8分）
为了了解某市在减轻学生作业负担的工作上的落实情况，该市教育局对某校某班每个同学晚上完成作业的时间进行了一次调查统计，并根据收集的数据绘制了如图所示的两幅不完整的统计图，请你根据图中提供的信息，完成下面的问题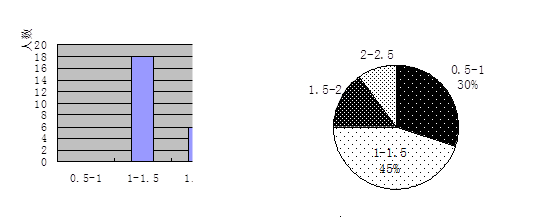
（1）该班共有多少学生？
（2）将图中的条形统计图补充完整
（3）求作业完成时间在0.5-1小时的部分对应扇形圆心角是多少度？
（4）如果该校七年级共有1000名学生，请估计七年级学生完成作业时间超过1.5小时的大约有多少人？
化简或化简求值（每小题6分，共12分）
（1）|a-2|+（b+3）2=0，求3a2b-[2ab2-2（ab-1.5a2b）+ab]+3ab2的值；
（2）已知有理数a、b、c在数轴上的对应点如图所示，化简：|b-a|+|a+c|-2|c-b|．
某食品加工厂需要一批食品包装盒，供应这种包装盒有两种方案可供选择：
方案1：从包装盒加工厂直接购买，购买所需的费用y1与包装盒数x满足如图的函数关系。
方案2：租赁机器自己加工，所需费用y2（包括租赁机器的费用和生产包装盒的费用）与包装盒数x满足如图的函数关系。
根据图象回答下列问题:
（1）方案1中每个包装盒的价格是多少元？
（2）方案2中租赁机器的费用是多少元？生产一个包装盒的费用是多少元？
（3）请分别求出y1,、y2与x的函数表达式；
（4）如果你是决策者，你认为应该选择哪种方案更省钱？并说明理由。
|
阅读理解题： 如图，在△ABC中，AD是BC边上的中线，且AD=
BC．
求证：∠BAC=90°．
证明：∵AD=BC，BD=CD=BC，
∴AD=BD=DC，
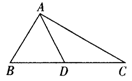
∴ADB和 ADC都是等腰三角形
∴∠B=∠BAD，∠C=∠CAD，
∵∠B+∠BAD+∠CAD+∠C=180°，
∴∠BAD+∠CAD=90°，即∠BAC=90°．
（1）此题实际上是直角三角形的另一个判定方法，请你用文字语言叙述出来．
（2）直接运用这个结论解答题目：一个三角形一边长为2，这边上的中线长为1，另两边之和为1+
，求这个三角形的面积．
【知识储备：勾股定理：在直角三角形中。两直角边的平方和等于斜边的平方。】
某校运动会需购买A、B两种奖品.若购买A种奖品3件和B种奖品2件，共需60元；若购买A种奖品5件和B种奖品3件，共需95元．
（1）求A、B两种奖品单价各是多少元？
（2）学校计划购买A、B两种奖品共100件，购买费用不超过1150元，且A种奖品的数量不大于B种奖品数量的3倍.设购买A种奖品m件，购买费用为W元，求出W（元）与m（件）之间的函数关系式，求出自变量m的取值范围，并确定最少费用W的值.
粤公网安备 44130202000953号