(本题满分12分)
某商店经销一种洗衣粉，年销售总量为6000包，每包进价为2.8元，销售价为3.4元，全年分若干次进货，每次进货均为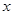
包，已知每次进货的运输劳务费为62.5元，全部洗衣粉一年的保管费为1.5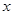元.
(1)将该商店经销洗衣粉一年的利润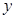
(元)表示为每次进货量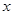(包)的函数；
(2)为使利润最大，每次应进货多少包？
，
，
，
．当
，
，
，
时，分别求点
的坐标．
的边长为１，
，
分别为边
，
上的点．当
的周长为２时，求
的大小．
，
是
，
之间的一定点，并且
，
．
是直线
．且使
与直线
，求
面积的最小值．
，
，求
的值．
，试用含
的式子表示
．推荐套卷
(本题满分12分)
某商店经销一种洗衣粉，年销售总量为6000包，每包进价为2.8元，销售价为3.4元，全年分若干次进货，每次进货均为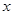包，已知每次进货的运输劳务费为62.5元，全部洗衣粉一年的保管费为1.5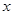元.
(1)将该商店经销洗衣粉一年的利润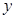(元)表示为每次进货量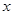(包)的函数；
(2)为使利润最大，每次应进货多少包？
粤公网安备 44130202000953号