（本小题满分13分）
如图M为的△ABC的中线AD的中点，过M的直线分别与边AB,AC交于点P,Q，设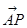
=x
，
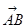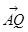=y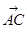
,记y=f(x)
（１）求函数y=f(x)的表达式；
（２）设g(x)=x3+3a2x+2a，(x∈[0,1]),若对于任意x1∈[
,1]，总存在x2∈[0,1]使得f(x1)=g(x2)成立，求实数a的取值范围；
相关试题
在
及
时取得极值．
，都有
成立，求c的取值范围．
，射线
与椭圆的交点为
，过
、
两点(异于
；
面积的最大值.
恒成立，求实数m的取值范围.
，
．
，求
的值．
，求
的单调的递减区间；推荐套卷
（本小题满分13分）
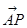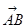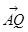如图M为的△ABC的中线AD的中点，过M的直线分别与边AB,AC交于点P,Q，设=x，=y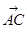,记y=f(x)
（１）求函数y=f(x)的表达式；
（２）设g(x)=x3+3a2x+2a，(x∈[0,1]),若对于任意x1∈[,1]，总存在x2∈[0,1]使得f(x1)=g(x2)成立，求实数a的取值范围；
粤公网安备 44130202000953号