在平面直角坐标系中，已知点A（4，0），点B（0，3）. 点P从点A出发，以每秒1个单位的速度向右平移，点Q从点B出发，以每秒2个单位的速度向右平移，又P、Q两点同时出发.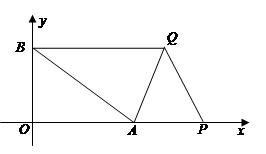
连结AQ，当△ABQ是直角三角形时，求点Q的坐标
当P、Q运动到某个位置时，如果沿着直线AQ翻折，点P恰好落在线段AB上，求这时∠AQP的度数
，其中x=2．
．
．相关知识点
推荐套卷
在平面直角坐标系中，已知点A（4，0），点B（0，3）. 点P从点A出发，以每秒1个单位的速度向右平移，点Q从点B出发，以每秒2个单位的速度向右平移，又P、Q两点同时出发.连结AQ，当△ABQ是直角三角形时，求点Q的坐标
当P、Q运动到某个位置时，如果沿着直线AQ翻折，点P恰好落在线段AB上，求这时∠AQP的度数
粤公网安备 44130202000953号