学校举行了“善行校园”的演讲比赛,赛后整理参赛同学的成绩,将学生的成绩分成 A、B、C、D四个等级,并制成了如下的条形统计图和扇形图(如图1、图2).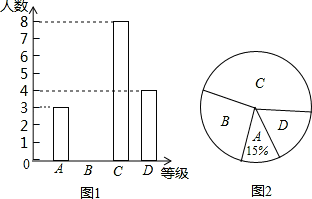
(1)补全条形统计图.
(2)学校决定从本次比赛中获得A和B的学生中各选出一名去参加市中学生环保演讲比赛.已知A等中男生有2名,B等中女生有3 名,请你用“列表法”或“树形图法”的方法求出所选两位同学恰好是一名男生和一名女生的概率.
相关知识点
推荐套卷
学校举行了“善行校园”的演讲比赛,赛后整理参赛同学的成绩,将学生的成绩分成 A、B、C、D四个等级,并制成了如下的条形统计图和扇形图(如图1、图2).
(1)补全条形统计图.
(2)学校决定从本次比赛中获得A和B的学生中各选出一名去参加市中学生环保演讲比赛.已知A等中男生有2名,B等中女生有3 名,请你用“列表法”或“树形图法”的方法求出所选两位同学恰好是一名男生和一名女生的概率.