如图,设P是圆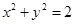 上的动点,点
上的动点,点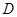 是
是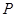 在
在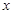 轴上的投影,
轴上的投影,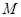 为线段PD上
为线段PD上 一点,且
一点,且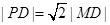 .点
.点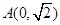 、
、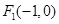 .
.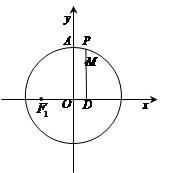
(1)设在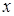 轴上存在定点
轴上存在定点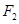 ,使
,使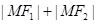 为定值,试求
为定值,试求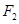 的坐标,并指出定值是多少?
的坐标,并指出定值是多少?
(2)求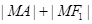 的最大值,并求此时点
的最大值,并求此时点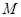 的坐标.
的坐标.
相关知识点
推荐套卷
如图,设P是圆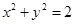 上的动点,点
上的动点,点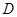 是
是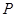 在
在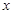 轴上的投影,
轴上的投影,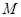 为线段PD上
为线段PD上 一点,且
一点,且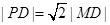 .点
.点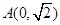 、
、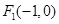 .
.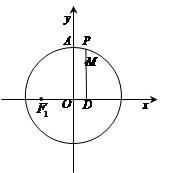
(1)设在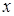 轴上存在定点
轴上存在定点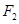 ,使
,使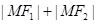 为定值,试求
为定值,试求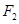 的坐标,并指出定值是多少?
的坐标,并指出定值是多少?
(2)求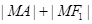 的最大值,并求此时点
的最大值,并求此时点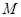 的坐标.
的坐标.