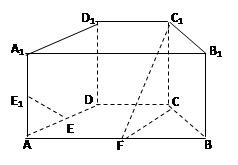（本小题满分12分）
如图，在直四棱柱ABCD-A
BCD中，底面ABCD为等腰梯形，AB//CD，AB="4," BC="CD=2, " AA="2, " E、E、F分别是棱AD、AA、AB的中点。
（1） 证明：直线EE
//平面FCC；
（2） 求二面角B-FC-C的余弦值。 
和等比数列
，且
，
，
，
，
，试比较
与
，
与
的大小，并猜想
与
（
，
能被
整除（其中
）．
．
的前
项和
，先计算数列的前4项，后猜想
并证明之．
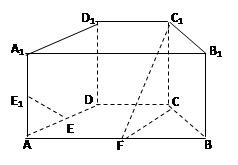
．推荐套卷
（本小题满分12分）
如图，在直四棱柱ABCD-ABCD中，底面ABCD为等腰梯形，AB//CD，AB="4," BC="CD=2, " AA="2, " E、E、F分别是棱AD、AA、AB的中点。
（1） 证明：直线EE//平面FCC；
（2） 求二面角B-FC-C的余弦值。
粤公网安备 44130202000953号