（本小题满分12分）如图四棱锥
的底面是正方形，
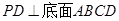，点E在棱PB上，O为AC与BD的交点。
（1）求证：平面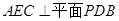
；
（
2）当E为PB中点时，求证：
//平面PDA，//平面PDC。
（3）当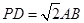
且E为PB的中点时，求
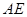与平面
所成的角的大小。
，
的最小值为
，求
的值
图像是否为中心对称图形
=
（
）定义域为
，若所有点（
）（
）构成一正方形，求
的值
，
在函数
的图像上，称
为函数
的一组关于原点的中心对称点，
关于原点的中心对称点有多少组
=
（
的对称中心为
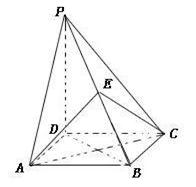
推荐套卷
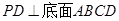（本小题满分12分）如图四棱锥的底面是正方形，，点E在棱PB上，O为AC与BD的交点。
（1）求证：平面；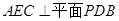
（2）当E为PB中点时，求证：//平面PDA，//平面PDC。
（3）当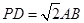且E为PB的中点时，求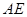与平面所成的角的大小。
粤公网安备 44130202000953号