某同学要把自己的计算机接入因特网，现有两家ISP公司可供选择，公司A每小时受费1.5元；公司B的收费规则如下：在用户上网的第1小时内收费1.7元，第2小时内收费1.6元，以后每小时减少0.1元（若超过17小时，按17小时计算）如图所示.
假设一次上网时间总小于17小时，那么，一次上网在多长时间以内能够保证选择公司A比选择公司B所需费用少？请写出其中的不等关系．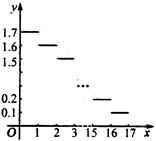
相关试题
,函数
．
的最小正周期
;
、
、
分别为
内角
、
、
的对边, 其中
,且
,求
和
中，底面
是直角梯形，
，
，
，
，
平面
．
平面
；
平面
；
是
的中点，求三棱锥
的体积．
的前
项和是
，且
．
，求数列
的前
，
.
，用列举法表示集合
；
，求以
内的概率.
，其中
.(Ⅰ)若
，求
在
上的最小值；
在定义域内既有极大值又有极小值，求实数
的取值范围；
，使得当
时，不等式
恒成立.推荐套卷
某同学要把自己的计算机接入因特网，现有两家ISP公司可供选择，公司A每小时受费1.5元；公司B的收费规则如下：在用户上网的第1小时内收费1.7元，第2小时内收费1.6元，以后每小时减少0.1元（若超过17小时，按17小时计算）如图所示.
假设一次上网时间总小于17小时，那么，一次上网在多长时间以内能够保证选择公司A比选择公司B所需费用少？请写出其中的不等关系．
粤公网安备 44130202000953号