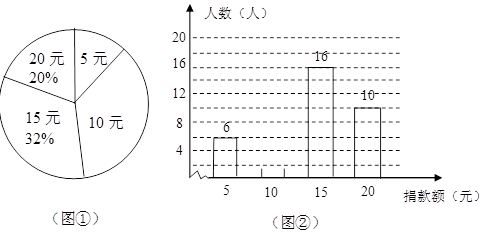
为支援“玉树抗震救灾”,在一次爱心捐款活动中,九(1)班同学人人拿出自己的零花钱,踊跃捐款,学生捐款额有5元、10元、15元、20元共四种情况.根据统计数据绘制了图①和图②两幅尚不完整的统计图.该班共有_____________名同学,学生捐款的众数是______________;
请你将图②的统计图补充完整;
计算该班同学平均捐款多少元?
从这个班任意抽取一名学生,这名学生捐款额为10元以上(不含10元)的概率是多少?
相关知识点
推荐套卷
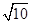 .
.
 有两个相等的实数根,求
有两个相等的实数根,求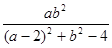 的值.
的值.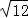 +|1﹣2
+|1﹣2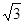 |+(π﹣
|+(π﹣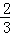 )0;
)0;
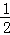 BC•r+
BC•r+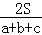 .
.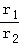 的值.
的值.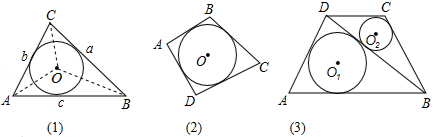
 粤公网安备 44130202000953号
粤公网安备 44130202000953号