(本题18 分)已知数列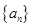 :
: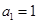 、
、 、
、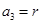 且
且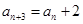 (
(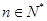 ),与数列
),与数列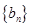 :
: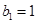 、
、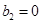 、
、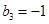 、
、 且
且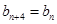 (
(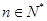 ).
).
记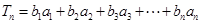 .
.
(1)若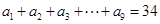 ,求
,求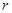 的值;
的值;
(2)求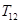 的值,并求证当
的值,并求证当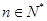 时,
时,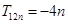 ;
;
(3)已知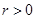 ,且存在正整数
,且存在正整数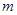 ,使得在
,使得在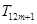 ,
,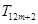 ,
,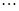 ,
, 中有4项为100。求
中有4项为100。求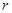 的值,并指出哪4项为100。
的值,并指出哪4项为100。
相关知识点
推荐套卷
(本题18 分)已知数列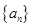 :
: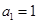 、
、 、
、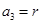 且
且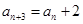 (
(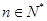 ),与数列
),与数列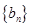 :
: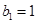 、
、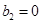 、
、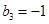 、
、 且
且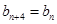 (
(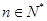 ).
).
记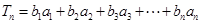 .
.
(1)若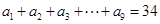 ,求
,求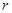 的值;
的值;
(2)求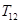 的值,并求证当
的值,并求证当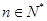 时,
时,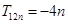 ;
;
(3)已知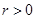 ,且存在正整数
,且存在正整数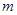 ,使得在
,使得在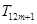 ,
,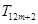 ,
,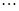 ,
,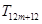 中有4项为100。求
中有4项为100。求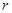 的值,并指出哪4项为100。
的值,并指出哪4项为100。