本题共有3个小题,第(1)小题满分4分,第(2)小题满分5
分,第(3)小题满分7分.
将边长分别为1、2、3、…、n、n+1、…(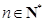 )的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为
)的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为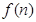 .记数列
.记数列 满足
满足 ,
,
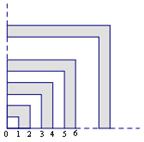
(1)求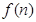 的表达式;
的表达式;
(2)写出 的值,并求数列
的值,并求数列 的通项公式;
的通项公式;
(3)记 ,若不等式
,若不等式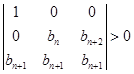 有解,求
有解,求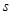 的取值范围.
的取值范围.
相关知识点
推荐套卷
本题共有3个小题,第(1)小题满分4分,第(2)小题满分5
分,第(3)小题满分7分.
将边长分别为1、2、3、…、n、n+1、…(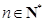 )的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为
)的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为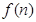 .记数列
.记数列 满足
满足 ,
,

(1)求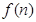 的表达式;
的表达式;
(2)写出 的值,并求数列
的值,并求数列 的通项公式;
的通项公式;
(3)记 ,若不等式
,若不等式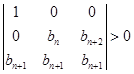 有解,求
有解,求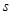 的取值范围.
的取值范围.