（本小题满分为１４分）
已知抛物线
的焦点为F，A、B是热线上的两动点，且
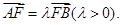过A、B两点分别作抛物线的切线，设其交点为M。
（I）证明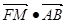
为定值；
（II）设
的面积为S，写出
的表达式，并求S的最小值。
相关试题
的焦点作一条斜率为k(k≠0)的弦，此弦满足：①弦长不超过8；②弦所在的直线与椭圆3x2+ 2y2= 2相交，求k的取值范围．
的右焦点F作直线l与双曲线C交于P、Q两点，
,求点M的轨迹方程．
上的两个动点，
是椭圆上一定点，
是其左焦点，且|PF|、|MF|、|QF|成等差数列。
和
，动点C到A、B两点的距离之差的绝对值为2，点C的轨迹与直线
交于D、E两点，求线段DE的长．相关知识点
推荐套卷
（本小题满分为１４分）
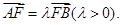已知抛物线的焦点为F，A、B是热线上的两动点，且过A、B两点分别作抛物线的切线，设其交点为M。
（I）证明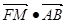为定值；
（II）设的面积为S，写出的表达式，并求S的最小值。
粤公网安备 44130202000953号