某电器公司生产A型电脑。1993年这种电脑每台平均生产成本为5 000元，并以纯利润20%确定出厂价。从1994年开始，公司通过更新设备和加强管理，使生产成本逐年降低。到1997年，尽管A型电脑出厂价仅是1993年的80%，但却实现了50%纯利润的高效益。
（1）求1997年每台A型电脑的生产成本；
（2）以1993年的生产成本为基数，求1993～1997年生产成本平均每年降低的百分数（精确到0.01，以下数据可供参考：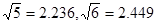
）。
相关试题
，
，
，求证：
的对棱
、
成
的角，且
，平行于
、
、
、
于
、
、
、
．
为平行四边形；
为平行四边形
所在平面外一点，
为
的中点，
平面
．
中，
是平行四边形，
，
分别是
，
的中点．
平面
．
、
、
分别为空间四边形
的边
，
，
上的点，且
．
平面
，
平面
的交线
．
推荐套卷
某电器公司生产A型电脑。1993年这种电脑每台平均生产成本为5 000元，并以纯利润20%确定出厂价。从1994年开始，公司通过更新设备和加强管理，使生产成本逐年降低。到1997年，尽管A型电脑出厂价仅是1993年的80%，但却实现了50%纯利润的高效益。
（1）求1997年每台A型电脑的生产成本；
（2）以1993年的生产成本为基数，求1993～1997年生产成本平均每年降低的百分数（精确到0.01，以下数据可供参考：）。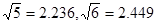
粤公网安备 44130202000953号