结合数轴与绝对值的知识回答下列问题:
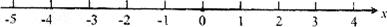
数轴上表示1和4的两点之间的距离是_________;表示-3和2的两点之间的距离是_________;表示-5和-4的两点之间的距离是_________;一般地,数轴上表示数
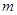 和数
和数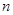 的两点之间的距离等于_____________.
的两点之间的距离等于_____________.
如果表示数
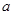 和-2的两点之间的距离是3,那么
和-2的两点之间的距离是3,那么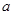 =__________.
=__________.
若数轴上表示数
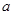 的点位于-4与2之间,求
的点位于-4与2之间,求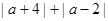 的值;
的值;
当
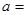 ______时,
______时,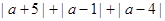 的值最小,最小值是____________
的值最小,最小值是____________
相关知识点
推荐套卷
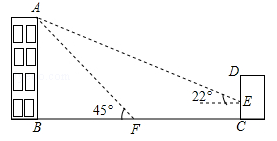
 ,cos22º≈
,cos22º≈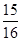 ,tan22º≈
,tan22º≈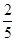 )
)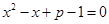 有两个实数根
有两个实数根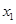 、
、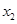 .
.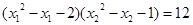 ,求p的值.
,求p的值. ,其中x是一元二次方程
,其中x是一元二次方程 的根.
的根.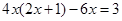
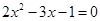 (用配方法)
(用配方法) 粤公网安备 44130202000953号
粤公网安备 44130202000953号