如图,已知 中,
中, 厘米,
厘米, 厘米,点
厘米,点 为
为 的中点.
的中点.
如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后, 与
与 是否全等,请说明理由;
是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使 与
与 全等?
全等?若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿
 三边运动,求经过多长时间点P与点Q第一次在
三边运动,求经过多长时间点P与点Q第一次在 的哪条边上相遇?
的哪条边上相遇?
相关知识点
推荐套卷
 ),两个不全等的等腰直角三角形
),两个不全等的等腰直角三角形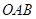 和
和 叠放在一起,并且有公共的直角顶点
叠放在一起,并且有公共的直角顶点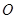 .
.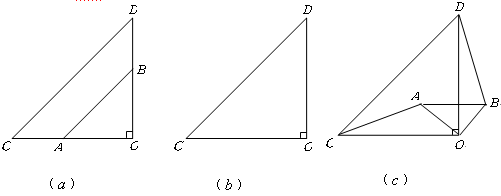
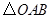 绕点
绕点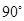 角,在图(
角,在图(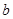 )中作出旋转后的
)中作出旋转后的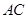 ,
,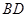 的数量关系是,直线
的数量关系是,直线 ),这时(2)中的两个结论是否成立?作出判断并说明理由.若
),这时(2)中的两个结论是否成立?作出判断并说明理由.若 的图像经过点A(-3,-1)和点B(-3,-9).
的图像经过点A(-3,-1)和点B(-3,-9).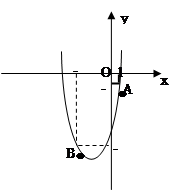

 ,以边BC为直径的半圆与边AB,AC分别交于点D、E,过点D作DF⊥AC于点F,
,以边BC为直径的半圆与边AB,AC分别交于点D、E,过点D作DF⊥AC于点F,
 粤公网安备 44130202000953号
粤公网安备 44130202000953号