二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下所示,相应图象如图所示,结合表格和图象回答下列问题: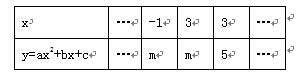
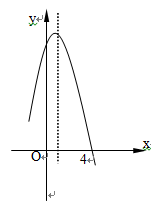
抛物线y=ax2+bx+c的对称轴是直线x= ;
方程ax2+bx+c=0的两根是x1= ,x2= ;
求出二次函数y=ax2+bx+c的解析式及m的值;
求当方程ax2+bx+c=k有解时k的取值范围.(结合图形直接写出答案)
相关知识点
推荐套卷
二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下所示,相应图象如图所示,结合表格和图象回答下列问题:

抛物线y=ax2+bx+c的对称轴是直线x= ;
方程ax2+bx+c=0的两根是x1= ,x2= ;
求出二次函数y=ax2+bx+c的解析式及m的值;
求当方程ax2+bx+c=k有解时k的取值范围.(结合图形直接写出答案)