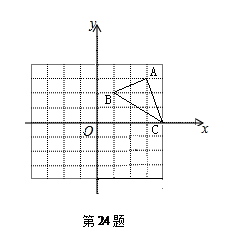
．如图，将腰长为的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限，其中点A在y轴上，点B在抛物线y＝ax2＋ax－2上，点C的坐标为(－1，0)．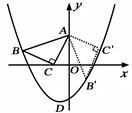
(1)点A的坐标为 ，点B的坐标为 ；
(2)抛物线的关系式为 ，其顶点坐标为 ；
(3)将三角板ABC绕顶点A逆时针方向旋转90°，到达
的位置．请判断点
、
是否在(2)中的抛物线上，并说明理由．
相关试题
如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．
（1）求证：四边形DBFE是平行四边形；
（2）当△ABC满足什么条件时，四边形DBEF是菱形？为什么？
，其中
.
如图，已知直线AB：
与抛物线
交于A、B两点，
（1）直线AB总经过一个定点C，请直接写出点C坐标；
（2）当
时，在直线AB下方的抛物线上求点P，使△ABP的面积等于5；
（3）若在抛物线上存在定点D使∠ADB＝90°，求点D到直线AB的最大距离.
相关知识点
推荐套卷
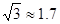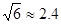粤公网安备 44130202000953号