(本题9分)用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形,设格点多边形的面积为S,它各边上格点的个数和为x。
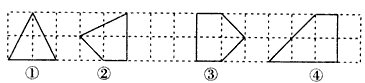
(1)如上图所示中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出S与x之间的关系式,答:S=_____。
多边形的序号
|
①
|
②
|
③
|
④
|
|
多边形的面积S
|
2
|
|
3
|
|
|
各边上格点的个数和x
|
4
|
5
|
6
|
|
|
(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有2个格点。
此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S=____。
(3)请你继续探索,当格点多边形内部有且只有n个格点时,猜想S与x有怎样的关系?