已知椭圆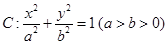 的离心率为
的离心率为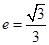 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线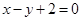 相切,
相切,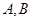 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点, 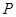 为椭圆
为椭圆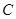 上的动点.
上的动点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)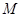 为过
为过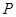 且垂直于
且垂直于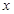 轴的直线上的点,若
轴的直线上的点,若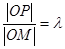 ,求点
,求点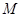 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
相关知识点
推荐套卷
已知椭圆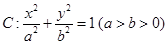 的离心率为
的离心率为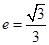 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线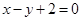 相切,
相切,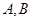 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点, 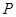 为椭圆
为椭圆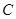 上的动点.
上的动点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)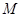 为过
为过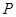 且垂直于
且垂直于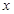 轴的直线上的点,若
轴的直线上的点,若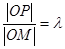 ,求点
,求点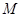 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.