甲、乙两人连续6年对某县农村甲鱼养殖业的规模（产量）进行调查，提供了两个方面的信息如下图所示。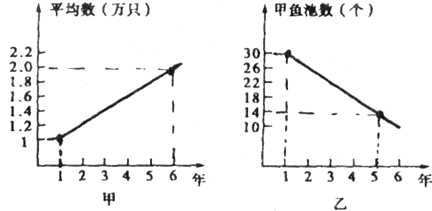
甲调查表明：每个甲鱼池平均出产量从第一年1万只甲鱼上升到第6年2万只。
乙调查表明：甲鱼池个数由第1年30个减少到第6年10个，请你根据提供的信息说明：
（1）第2年甲鱼池的个数及全县出产甲鱼总数；
（2）到第6年这个县的甲鱼养殖业的规模比第1年是扩大了还是缩小了？说明理由；
（3）哪一年的规模最大？说明理由
相关试题
.
的最小正周期和单调递减区间；
上的值域.
}是等差数列，且
=12，
=27，
}的前
项和
，曲线
在点
处的切线方程为
。
、
的值；
，且
时，
，求
的取值范围
.
在点
处的切线方程；
在区间
上均为增函数，求
的取值范围；
有唯一解，试求实数
的值.
在
上存在单调递增区间，求
的取值范围；
上的最值.推荐套卷
甲、乙两人连续6年对某县农村甲鱼养殖业的规模（产量）进行调查，提供了两个方面的信息如下图所示。
甲调查表明：每个甲鱼池平均出产量从第一年1万只甲鱼上升到第6年2万只。
乙调查表明：甲鱼池个数由第1年30个减少到第6年10个，请你根据提供的信息说明：
（1）第2年甲鱼池的个数及全县出产甲鱼总数；
（2）到第6年这个县的甲鱼养殖业的规模比第1年是扩大了还是缩小了？说明理由；
（3）哪一年的规模最大？说明理由
粤公网安备 44130202000953号