某新设备M在第1年可以生产价值120万元的产品,在使用过程中,由于设备老化及维修原因使得M的生产能力逐年减少,从第2年到第6年,每年M生产的产品价值比上年减少10万元;从第7年开始,每年M生产的产品价值为上年的75%.
(I)求第n年M生产的产品价值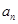 的表达式;
的表达式;
(II)该设备M从购买回来后马上使用,则连续正常使用10年可以生产多少价值的产品?
推荐套卷
某新设备M在第1年可以生产价值120万元的产品,在使用过程中,由于设备老化及维修原因使得M的生产能力逐年减少,从第2年到第6年,每年M生产的产品价值比上年减少10万元;从第7年开始,每年M生产的产品价值为上年的75%.
(I)求第n年M生产的产品价值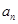 的表达式;
的表达式;
(II)该设备M从购买回来后马上使用,则连续正常使用10年可以生产多少价值的产品?