某地需要修建一条大型输油管道通过120公里宽的沙漠地带，该段输油管道两端的输油站已建好，余下工程只需要在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站（又称泵站）.经预算，修建一个增压站的工程费用为432万元，铺设距离为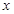
公里的相邻两增压站之间的输油管道费用为
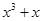万元.设余下工程的总费用为
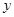万元.
（1）试将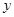表示成关于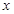的函数；
（2）需要修建多少个增压站才能使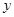最小？
，集合
．
时，
； (2) 若
，求实数
的取值范围．
和直线
的交点
的坐标，及点
的距离。
；
；
的单调递增区间； 
求函数
的最值及对应的
在
的取值范围.
的方程
，求方程有实根的概率；
，求方程有实根的概率.推荐套卷
某地需要修建一条大型输油管道通过120公里宽的沙漠地带，该段输油管道两端的输油站已建好，余下工程只需要在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站（又称泵站）.经预算，修建一个增压站的工程费用为432万元，铺设距离为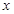公里的相邻两增压站之间的输油管道费用为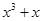万元.设余下工程的总费用为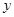万元.
（1）试将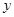表示成关于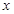的函数；
（2）需要修建多少个增压站才能使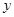最小？
粤公网安备 44130202000953号