(本小题满分12分)
已知 F1、F2是椭圆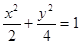
的两焦点，
是椭圆在第一象限弧上一点，且满足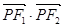
=1.过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
（1）求P点坐标;
（2）求证直线AB的斜率为定值;
（3）求△PAB面积的最大值.
为锐角，若
试求
的值.
；
的大小,并证明
证明你的结论。
推荐套卷
(本小题满分12分)
已知 F1、F2是椭圆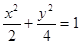的两焦点，是椭圆在第一象限弧上一点，且满足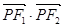=1.过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
（1）求P点坐标;
（2）求证直线AB的斜率为定值;
（3）求△PAB面积的最大值.
粤公网安备 44130202000953号