（本题12分）△ABC中，∠A=∠B=30°，AB=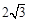
．把△ABC放在平面直角坐标系中，使AB的中点位于坐标原点O (如图)，△ABC可以绕点O作任意角度的旋转．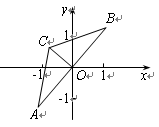
(1) 当点B在第一象限，纵坐标是
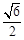时，求点B的横坐标；(2) 如果抛物线
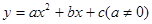的对称轴经过点C，请你探究：
①当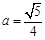
，
，
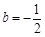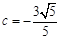时，A，B两点是否都在这条抛物线上？并说明理由；
②设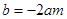
，是否存在这样的m的值，使A，B两点不可能同时在这条抛物线上？若存在，直接写出m的值；若不存在，请说明理由．
相关试题
如图，平面上有三点A、B、C，按要求画图：
(1)连接AB；
(2)作直线AC；
(3)作射线CB；
(4)过点C作线段AB的垂线，垂足为D；
(5)量出点C到线段AB的距离是 ▲ (精确到mm)
，其中
如图，直线AB与CD相交于点O，OP是∠BOC的平分线，OE⊥AB，OF⊥CD，
(1)图中除直角外，还有相等的角吗？请写出两对：① ▲ ；② ▲ ．
(2)如果∠AOD= 40º，则①∠BOC=" " ▲ ；
②OP是∠BOC的平分线，所以∠COP=" " ▲ 度；
③求∠BOF的度数．
； 
相关知识点
推荐套卷
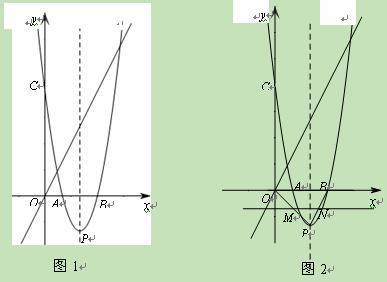
粤公网安备 44130202000953号