（本小题9分）如图、在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE。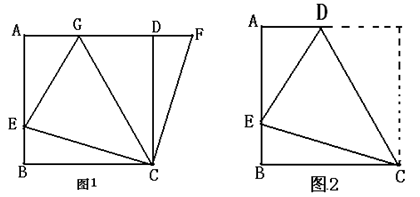
（1）求证：CE=CF
(2)在图1中，若G在AD上，且∠GCE=45°,则GE=BE+GD成立吗？为什么？
（3）运用（1）（2）解答中积累的经验和知识，完成下题：
如图2，四边形ABCD中，AD∥BC(BC＞AD),∠B=90°,AB=BC=12,E是AB上一点，
且∠DCE=45°，BE=4，求DE的 长。
，乙写出的解是
．你找出的与甲、乙不相同的一组解是 ．
可化为两个方程组 
的解是 ．
的解是 ．相关知识点
推荐套卷
（本小题9分）如图、在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE。（1）求证：CE=CF
(2)在图1中，若G在AD上，且∠GCE=45°,则GE=BE+GD成立吗？为什么？
（3）运用（1）（2）解答中积累的经验和知识，完成下题：
如图2，四边形ABCD中，AD∥BC(BC＞AD),∠B=90°,AB=BC=12,E是AB上一点，
且∠DCE=45°，BE=4，求DE的 长。
粤公网安备 44130202000953号