如图所示,在梯形ABCD中,已知AB∥DC, AD⊥DB,AD=DC=CB,
AB=4.以AB所在直线为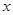 轴,过D且垂直于AB的直线为
轴,过D且垂直于AB的直线为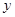 轴建立平面直角坐标系.
轴建立平面直角坐标系.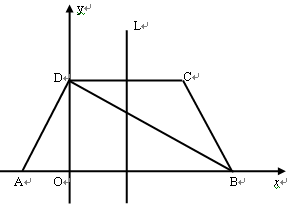
(1)求∠DAB的度数及A、D、C三点的坐标;
(2)求过A、D、C三点的抛物线的解析式及其
对称轴L.(3)若P是抛物线的对称轴L上的点,那么使
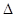 PDB为等腰三角形的点P有几个?
PDB为等腰三角形的点P有几个?
(不必求点P的坐标,只需说出个数即可)
相关知识点
推荐套卷
如图所示,在梯形ABCD中,已知AB∥DC, AD⊥DB,AD=DC=CB,
AB=4.以AB所在直线为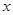 轴,过D且垂直于AB的直线为
轴,过D且垂直于AB的直线为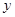 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求∠DAB的度数及A、D、C三点的坐标;
(2)求过A、D、C三点的抛物线的解析式及其
对称轴L.(3)若P是抛物线的对称轴L上的点,那么使
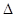 PDB为等腰三角形的点P有几个?
PDB为等腰三角形的点P有几个?
(不必求点P的坐标,只需说出个数即可)