已知 是边长为
是边长为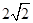 的正方形ABCD的中心,点E、F分别是AD、BC的中点,沿对角线AC把正方形ABCD折成直二面角D-AC-B;
的正方形ABCD的中心,点E、F分别是AD、BC的中点,沿对角线AC把正方形ABCD折成直二面角D-AC-B;
(Ⅰ)求∠EOF的大小;
(Ⅱ)求二面角E-OF-A的余弦值;
(Ⅲ)求点D到面EOF的距离.
推荐套卷
已知 是边长为
是边长为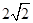 的正方形ABCD的中心,点E、F分别是AD、BC的中点,沿对角线AC把正方形ABCD折成直二面角D-AC-B;
的正方形ABCD的中心,点E、F分别是AD、BC的中点,沿对角线AC把正方形ABCD折成直二面角D-AC-B;
(Ⅰ)求∠EOF的大小;
(Ⅱ)求二面角E-OF-A的余弦值;
(Ⅲ)求点D到面EOF的距离.