若椭圆C1：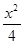
＋
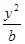＝1(0<b<2)的离心率等于
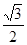，抛物线C2：x2＝2py(p>0)的焦点在椭圆C1的顶点上．
(Ⅰ)求抛物线C2的方程；
(Ⅱ)若过M(－1,0)的直线l与抛物线C2交于E、F两点，又过E、F作抛物线C2的切线l1、l2，当l1⊥l2时，求直线l的方程．
和复平面的点Z（
）对应，
、
必须满足什么条件，才能使点Z位于：（1）实轴上？（2）虚轴上？（3）上半平面（含实轴）？（4）左半平面（不含虚轴及原点）？
（
），
，当
取何值时，（1）
；（2）
分别取什么值时，复数
是（1）实数（2）虚数（3）纯虚数。
，求
的最大值和最小值．
的方程
有实根，求实数
的取值。推荐套卷
若椭圆C1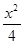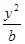：＋＝1(0<b<2)的离心率等于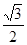，抛物线C2：x2＝2py(p>0)的焦点在椭圆C1的顶点上．
(Ⅰ)求抛物线C2的方程；
(Ⅱ)若过M(－1,0)的直线l与抛物线C2交于E、F两点，又过E、F作抛物线C2的切线l1、l2，当l1⊥l2时，求直线l的方程．
粤公网安备 44130202000953号