某小区要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水,连喷头在内,柱高为0.8m,水流各个方向上沿形状相同的抛物线路径落下,如图1所示。根据设计图纸已知:在图2所示直角坐标系中水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是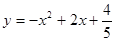 .
.
喷出的水流距水平面的最大高度是多少?

相关知识点
推荐套卷
某小区要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水,连喷头在内,柱高为0.8m,水流各个方向上沿形状相同的抛物线路径落下,如图1所示。根据设计图纸已知:在图2所示直角坐标系中水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是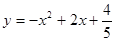 .
.
喷出的水流距水平面的最大高度是多少?
