如图,已知直线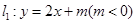 与抛物线
与抛物线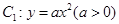 和圆
和圆 都相切,F是C1的焦点.
都相切,F是C1的焦点.
(1)求m与a的值;
(2)设A是C1上的一动点,以A为切点作抛物线C1的切线l,直线l交y轴于点B,以FA、FB为邻边作平行四边形FAMB,证明:点M在一条定直线上;
(3)在(2)的条件下,记点M点所在的定直线为l2,直线l2与y轴交点为N,连接MF交抛物线C1于P、Q两点,求△NPQ的面积S的取值范围.
相关知识点
推荐套卷
如图,已知直线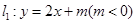 与抛物线
与抛物线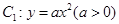 和圆
和圆 都相切,F是C1的焦点.
都相切,F是C1的焦点.
(1)求m与a的值;
(2)设A是C1上的一动点,以A为切点作抛物线C1的切线l,直线l交y轴于点B,以FA、FB为邻边作平行四边形FAMB,证明:点M在一条定直线上;
(3)在(2)的条件下,记点M点所在的定直线为l2,直线l2与y轴交点为N,连接MF交抛物线C1于P、Q两点,求△NPQ的面积S的取值范围.