.如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△A
BE是等腰直角三角形，AB=AE，FA=FE，∠AEF=40°
（1）求证：EF⊥平面BCE；
（2）设线段CD、AE的中点分别为P、M，求证：PM∥平面BCE
（3）求二面角F—BD—A的大小。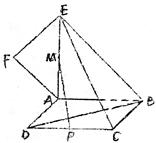
相关试题
＞
＞
与直线
交于
、
两点，且
，其中
为坐标原点．
的值；
，求椭圆的离心率
的取值范围．
轴上，其离心率
，已知点
到双曲线上的点的最短距离为
，求双曲线的方程．
和圆
，直线
与圆
相切于点
，圆
上，圆
，且被直线
．
表示一个圆．
的取值范围；
的轨迹方程．
经过点
，直线
经过点
时，试判断直线
的值．推荐套卷
.如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△ABE是等腰直角三角形，AB=AE，FA=FE，∠AEF=40°
（1）求证：EF⊥平面BCE；
（2）设线段CD、AE的中点分别为P、M，求证：PM∥平面BCE
（3）求二面角F—BD—A的大小。
粤公网安备 44130202000953号