如图，某小区有一长为30m，宽为20m的广场，图案如下，其中白色区域四周出口的宽度一样．小明在规定地点随意向图案内投掷小球，每球都能落在图案内，经过多次试验，发现落在黑色区域的概率是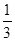
,那么白色区域四周出口的宽度应是多少？
相关试题
的值．
中恰有三个数相等，求
的值．
，求
的值.
；
；
；…………
＝ ；
．相关知识点
推荐套卷
如图，某小区有一长为30m，宽为20m的广场，图案如下，其中白色区域四周出口的宽度一样．小明在规定地点随意向图案内投掷小球，每球都能落在图案内，经过多次试验，发现落在黑色区域的概率是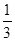,那么白色区域四周出口的宽度应是多少？
粤公网安备 44130202000953号