如图四棱锥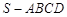
，底面四边形ABCD满足条件
，
，侧面SAD垂直于底面ABCD，
，
（1）若SB上存在一点E，使得
平面SAD，求
的值；
（2）求此四棱锥体积的最大值；
（3）当体积最大时，求二面角A-SC-B大小的余弦值．
相关试题
满足
。
， 
为
项和，求
。
的内角
所对的边分别为
且
。
，求
的值；
，求
的值。
与
的等比中项为
，
．推荐套卷
如图四棱锥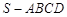，底面四边形ABCD满足条件，，侧面SAD垂直于底面ABCD，，
（1）若SB上存在一点E，使得平面SAD，求的值；
（2）求此四棱锥体积的最大值；
（3）当体积最大时，求二面角A-SC-B大小的余弦值．
粤公网安备 44130202000953号