(本题12分)△ABC中,∠A,∠B,∠C的对边分别为a,b,c,关于x的方程x2-2ax+b2=0的两根为x1、x2,x轴上两点M、N的坐标分别为(x1,0)、(x2,0),其中M的坐标是(a+c,0);P是y轴上一点,点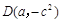 。
。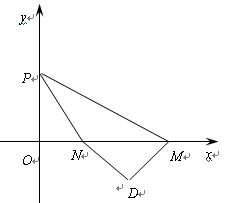
(1)试判断△ABC的形状,并说明理由;
(
 2)若S△MNP=3S△NOP, ①求sinB的值; ②判断△ABC的三边长能否取一组适当的值,使△
2)若S△MNP=3S△NOP, ①求sinB的值; ②判断△ABC的三边长能否取一组适当的值,使△ MND是等腰直角三角形?如能,请求出这组值;如不能,请说明理由.
MND是等腰直角三角形?如能,请求出这组值;如不能,请说明理由.
相关知识点
推荐套卷
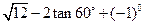 .
.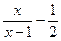 =0
=0 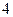 ,
,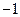 )的抛物线交
)的抛物线交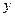 轴于
轴于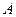 点,交
点,交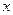 轴于
轴于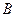 ,
,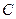 两点(点
两点(点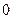 ,
,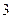 )。
)。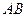 的垂线交抛物线于点
的垂线交抛物线于点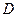 ,如果以点
,如果以点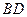 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴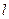 与⊙
与⊙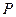 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于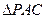 的面积最大?并求出此时
的面积最大?并求出此时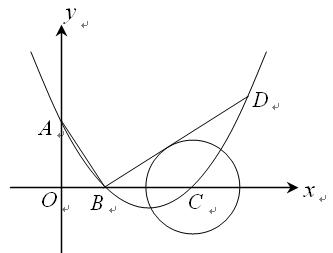
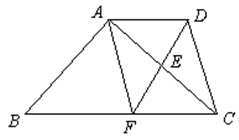
 几何直观性来阐明数之间的某种关系,即“以形助数”。如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
几何直观性来阐明数之间的某种关系,即“以形助数”。如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB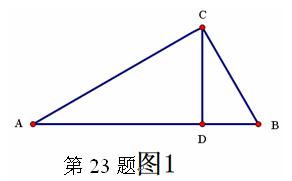
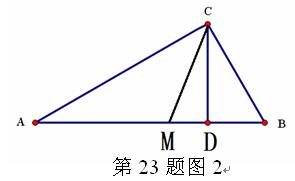
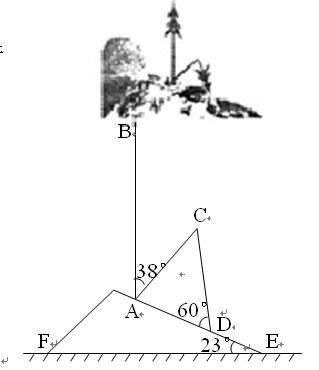
 被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m。
被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m。 ,
, ,
,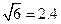 ).
).
 粤公网安备 44130202000953号
粤公网安备 44130202000953号